LeetCode算法题总结

发表于 2022/01/20

作者 裘俊云 24 分钟阅读

跟着代码随想录进行复习

数组

二分查找

一定要注意区间的设定，区间设定好，每一次的二分查找的left和right要遵循这个规则

例如 left = 0, right = length -1, 也就是[left, right]的情况，那二分之后 middle = (left + right) / 2

nums[middle] < nums[right] 则 right = middle - 1，而不是right = middle。并且while条件是 left <= right。

再例如 left = 0, right = length，也就是[left, right)的情况，那二分之后 middle = (left + right) / 2

nums[middle] < nums[right] 则 right = middle。而不是right = middle - 1。并且while条件是 left < right。

哈希表

两数之和

查给定数组中两数只和为target的算法，m+n=target

使用map[value]=index的哈希表进行存储，判断当前值m与target的差值n是否已经存在来判断是否存在两数只和为target的情况

简要写法就是 map[target-m] 有值，那就是m的下标和map[target-m]就是答案

242. 有效的字母异位词

这题感觉更像是考swift语法，两种思路，一种把字符串拆解成字符数组并排序，然后依次进行比较，如下，比较耗资源

学会使用map和sorted

  
func isAnagram(_ s: String, _ t: String) -> Bool {
  if s.count != t.count {
    return false
  }

  let sc = s.map { $0 }.sorted { $0 > $1 }
  let tc = t.map { $0 }.sorted { $0 > $1 }
  for i in 0..<s.count {
    if sc[i] != tc[i] {
      return false
    }
  }
  return true
}

第二种，利用哈希表（数组），字符对应26位字母，使用26长度的数组，下标为各字母所在位置，s表遍历+1，t表遍历-1，最后数组全部是0则是true

学会使用unicodeScalars

  
func isAnagram(_ s: String, _ t: String) -> Bool {
  if s.count != t.count {
    return false
  }
  var result: [Int] = [Int](repeating: 0, count: 26)
  let start = "a".unicodeScalars.first!.value
  for sc in s.unicodeScalars {
    result[Int(sc.value - start)] += 1
  }
  for tc in t.unicodeScalars {
    result[Int(tc.value - start)] -= 1
  }
  for r in result {
    if r != 0 {
      return false
    }
  }
  return true
}

454. 四数相加 II

四个数组，四数相加，先遍历加前两个数组的和sum，并将0-sum的值当key，value为出现0-sum的次数。

第二次遍历剩下的两个数组，和出现在sum的次数进行累加就是我们需要的结果

383. 赎金信

还是需要熟悉字符串的字符遍历，可以使用String.indices方法进行遍历，将第一个String各字符出现的次数使用map进行累加，再遍历第二个字符进行相减即可

双指针

移除元素

使用双指针，两个指针都跑动，慢指针用来指向正确的数字，快指针用来找出正确的数字

0 1 2 2 3 0 4 2，去除2

nums[quickI] != 2的情况下nums[slowI] = nums[quickI] slowI移动一位， quickI保持遍历移动

有序数组的平方

使用双指针，左右两端，向中间聚拢，大的放在新数组的最右边

15. 三数之和

先将数组进行低高排序，一个指针i从左往右固定遍历，另外两个指针left和right在i的右边进行滑动缩小

344. 反转字符串

比较简单，tmp=i,i=j,j=tmp进行交换即可

剑指 Offer 05. 替换空格

先算出空格的数量，然后将字符数组进行扩容，然后使用倒序遍历的方法，逐步插入

和字符串和链表的题目有很多重叠的部分

滑动窗口

长度最小的子数组

求n个正整数中，满足连续子数组和>=target的最小长度

使用滑动窗口的形式，其实也就是双支指针，只是这里的指针是取的两指针之间的数组计算。

右指针向右边移动，左指针当待定，一旦出现right到left的和>=target，记录下宽度，并left又移，直到right已经在最右边且left到right和<target情况，结束滑动

无重复字符的最长子串

链表

203. 移除链表元素

相对简单，注意swift写法写的opthonal即可

206. 反转链表

三个指针，一个指向当前，一个指向next，一个指向next的next即可

24. 两两交换链表中的节点

用一个递归算法解决问题，反转 n1和n2，n1的next就是余下链表的反转

19. 删除链表的倒数第 N 个结点

这里需要注意的就是要在前端建立一个自己的虚拟头部节点，并当做新的head，使用快慢双指针的形式去计算快慢之间的宽度，最后返回虚拟头部节点的next

面试题 02.07. 链表相交

a1 a2 c1 c2 c3 null b1 b2 b3 c1 c2 c3 null

b1 b2 b3 c1 c2 c3 null a1 a2 c1 c2 c3 null

画八字跑圈，碰到一起的地方就是相交的地方

142. 环形链表 II

先使用快慢节点，快的一次走两步，慢的一次走一步，找到相交的节点，然后以head和这个相交的节点用相同的速度，每次走一步的方式，找到相交的节点就是入环的第一个节点

1 2 3 4 5 6 7 8 9，其中6为环形入口

// 第一遍快慢指针走
1 3 5 7 9 7 9 7 9 7 9
1 2 3 4 5 6 7 8 9 6 7
// 算出9位交集
// 1 9开始跑
1 2 3 4 5 6
9 6 7 8 9 6
// 算出6

字符串

344. 反转字符串

比较简单，tmp=i,i=j,j=tmp进行交换即可

剑指 Offer 05. 替换空格

先算出空格的数量，然后将字符数组进行扩容，然后使用倒序遍历的方法，逐步插入

剑指 Offer 58 - II. 左旋转字符串

反转左边，反转右边，然后整体反转

abcdefg，k=2。-> ba gfedc -> cdefgab。

这里要注意swift语法，inout 修饰入参变量，代表该入参变量是可修改的，赋值地方需要用取地址&符号

28. 找出字符串中第一个匹配项的下标中等难度前缀表解法

前缀表解法。前缀表是需要匹配字符串的一个前缀相等表。举例子，需要找出匹配aadaaf的第一个index。aadaaf的前缀表就是如下：

重点理解前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串；表中存的值是前缀的长度（也就是最后一个字符的下标+1）-1，减1就正好是下标，我们就按下标进行存储

  
str=aadaaf
010120
// str[0]前缀为空所以是0，str[1]可以找到前后缀相等的str[0]=str[1]所以为1，str[2]找不到所以0，str[3]可以找到前后缀相等的str[0]=str[3]所以为1,str[4]可以找到前后缀相等的str[0-1]=str[3-4]所以为2,str[5]找不到所以为0
str=asdasffg
00012010
// str[4]前后缀相等的str[0-1]=str[3-4]所以是2

先写出前缀表的计算函数

  
//前缀表统一减一
func getNext(_ next: inout [Int], needle: [Character]) {
    
    var j: Int = -1
    next[0] = j
    
    // i 从 1 开始
    for i in 1 ..< needle.count { // 注意i从1开始
        while j >= 0 && needle[i] != needle[j + 1] { // 前后缀不相同了
            j = next[j] // 向前回退。needle[i] 与 needle[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
        }
        if needle[i] == needle[j + 1] { // 找到相同的前后缀
            j += 1;
        }
        next[i] = j// 将j（前缀的长度）赋给next[i]
    }
    print(next)
}

  
func strStr(_ haystack: String, _ needle: String) -> Int {
    
    let s = Array(haystack), p = Array(needle)
    guard p.count != 0 else { return 0 }
    
    // 2 pointer
    var j = -1
    var next = [Int](repeating: -1, count: needle.count)
    // KMP
    getNext(&next, needle: p)
    for i in 0 ..< s.count {
        while j >= 0 && s[i] != p[j + 1] {
            //不匹配之后寻找之前匹配的位置
            j = next[j]
        }
        if s[i] == p[j + 1] {
            //匹配，双指针同时后移
            j += 1
        }
        if j == (p.count - 1) {
            //出现匹配字符串
            return i - p.count + 1
        }
    }
    return -1
}

位运算

344. 反转字符串

a = a ^ b

b = a ^ b = (a ^ b) ^ b = a

a = a ^ b = (a ^ b) ^ a = b

注意swift没有字符的位运算，只有int的，这里需要用到元组 (a, b) = (b, a)

堆栈

232. 用栈实现队列

swift用两个数组模拟栈，数组只能用append()函数和popLast方法。

一个数组存in，一个存out，out为空的话，就将in一个个放入到out中然后在pop

20. 有效的括号

匹配，制定字典，逐个进栈

二叉树相关的都会涉及到一点栈操作

二叉树

二叉树的遍历方式

144. 二叉树的前序遍历

先遍历中间节点，输入并入栈，看左边有就继续深入，无则取右节点继续，左右节点都没有则pop

94. 二叉树的中序遍历

145. 二叉树的后序遍历

102. 二叉树的层序遍历

一个先进先出队列，一个记录每层值数量的count，然后一层层遍历即可，这里要注意队列里面array的popFirst()方法不好使

226. 翻转二叉树

递归最好计算，然后还可以用层序遍历的迭代方法

101. 对称二叉树

迭代算法left=right，表示left.left==right.right && left.right==right.left，或是用栈进行分层遍历

104. 二叉树的最大深度

遍历，深度等于1+左边的深度和右边深度的最大值

二叉树的属性

二叉树的修改和改造

求二叉树的属性

二叉树公共祖先问题

二叉搜索树的修改与构造

回溯算法

其实就是递归算法

贪心算法

最小优解就是最大优解

455. 分发饼干

最小的饼干给最小刚好能吃这块就饱了的小孩吃

376. 摆动序列

模拟成上下坡的草图，连续上坡和连续下坡去掉中间的破段，不影响整个结果，也就是贪心。

主要平坡的特殊情况，上下中间是平坡，连续上坡中间是平坡，连续下坡中间有平坡的情况

前缀表

28. 找出字符串中第一个匹配项的下标

前缀表next数组真的是需要足够理解，梳理看到的两种解答的汇总理解

一个是代码随想录的；一个是在CSDN上的。

整体最不能理解的就是，不相等的情况下，回溯j=next[j]，是最不能理解的。

用代码随想录的说法：

如果 s[i] 与 s[j+1]不相同，也就是遇到前后缀末尾不相同的情况，就要向前回溯。怎么回溯呢？ next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。

两眼一抹黑，根本没有讲清楚，我们从另一篇文章看下

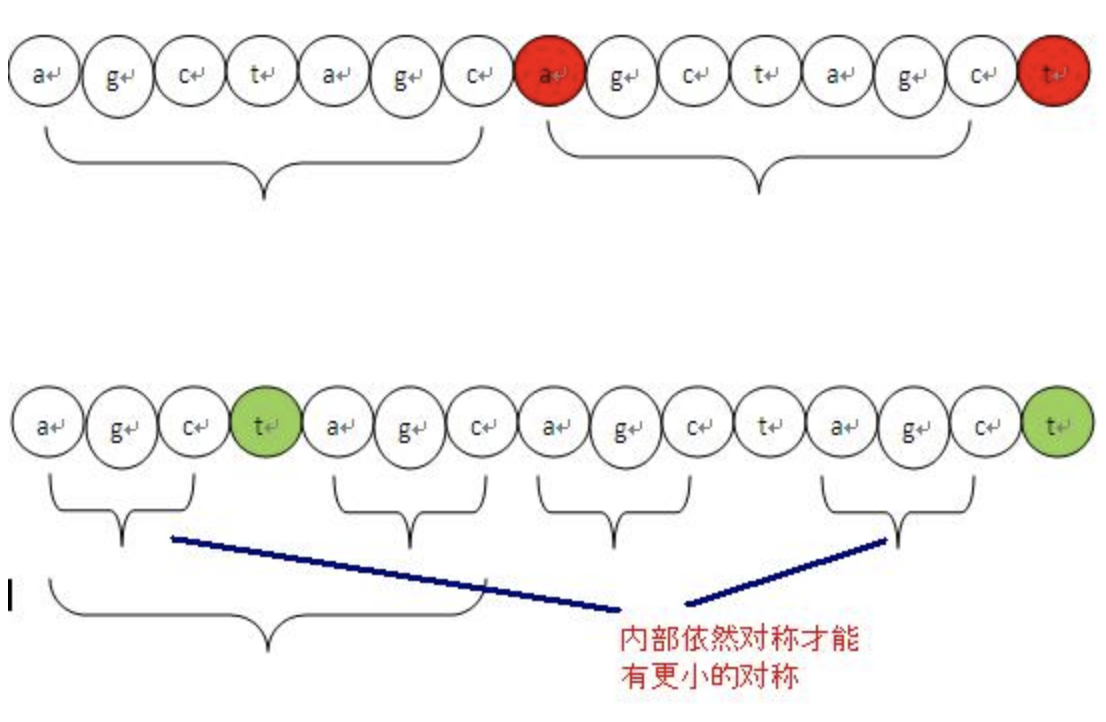
1、s[i] 如果要存在对称性，那么对称程度肯定比前面这个s[i-1]的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么s[i]就继承前面的对称性了。
2、要找更小的对称，必然在对称内部还存在子对称，而且这个s[i]必须紧接着在子对称之后。

也就是引用一个图，对于needle为 agctagcagctagctg的next数组

我们next数组求解的代码如下：

  
    /// 求解 next 数组
    func getNext(_ p: [Character]) -> [Int] {
        var j = -1
        var next = Array<Int>(repeating: 0, count: p.count)
        next[0] = j
        for i in 1..<p.count {// 注意i从1开始
            print("开始：j+1=\(j+1); i=\(i)")
            while j >= 0 && p[i] != p[j + 1] {// 前后缀不相同了
                j = next[j]// 向前回溯
                print("回溯：j+1=\(j+1)")
                
            }
            if p[i] == p[j+1] {// 找到相同的前后缀
                j += 1
            }
            next[i] = j// 将j（前缀的长度）赋给next[i]
            print("结束：j+1=\(j+1); i=\(i)")
            print("Next: \(p)")
            print("Next: \(next)")
        }

        print(next)
        return next
    }

agctagcagctagctg的next数组的执行过程

  
开始：j+1=0; i=1
结束：j+1=0; i=1
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=0; i=2
结束：j+1=0; i=2
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=0; i=3
结束：j+1=0; i=3
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=0; i=4
结束：j+1=1; i=4
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=1; i=5
结束：j+1=2; i=5
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=2; i=6
结束：j+1=3; i=6
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=3; i=7 // t != a && j > -1 触发回溯
// 找到agc(t)和agc(a)中的前一个字母也就是agc中的的最小对称子串就是 a，也就是j=next[j]
回溯：j+1=0 // j + 1 = next[2] + 1 = -1 + 1 = 0，s[j+1] == s[i] = s[0] == s[7]
结束：j+1=1; i=7
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=1; i=8
结束：j+1=2; i=8
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 0, 0, 0, 0, 0, 0, 0]
开始：j+1=2; i=9
结束：j+1=3; i=9
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 0, 0, 0, 0, 0, 0]
开始：j+1=3; i=10
结束：j+1=4; i=10
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 0, 0, 0, 0, 0]
开始：j+1=4; i=11
结束：j+1=5; i=11
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 0, 0, 0, 0]
开始：j+1=5; i=12
结束：j+1=6; i=12
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 5, 0, 0, 0]
开始：j+1=6; i=13
结束：j+1=7; i=13
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 0, 0]
// 重点看这里指向 a 和倒数第二个t 的时候回溯
开始：j+1=7; i=14
回溯：j+1=3 // 回溯到j+1=next[6]+1=3, 也就是前一个字符的最大子串agctagc(a) 和agctagc(t)中的agc
// next[j+1] = t == s[i] 也就是s[i]继承这里的对称性 next[i] = j + 1
结束：j+1=4; i=14 // j i 右偏移
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 3, 0]
开始：j+1=4; i=15
回溯：j+1=0
结束：j+1=0; i=15
needle: ["a", "g", "c", "t", "a", "g", "c", "a", "g", "c", "t", "a", "g", "c", "t", "g"]
Next: [-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 3, -1]
[-1, -1, -1, -1, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 3, -1]

agatagac的执行过程

  
开始：j+1=0; i=1
结束：j+1=0; i=1
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, 0, 0, 0, 0, 0]
开始：j+1=0; i=2
结束：j+1=1; i=2
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, 0, 0, 0, 0, 0]
开始：j+1=1; i=3
回溯：j+1=0
结束：j+1=0; i=3
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, -1, 0, 0, 0, 0]
开始：j+1=0; i=4
结束：j+1=1; i=4
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, -1, 0, 0, 0, 0]
开始：j+1=1; i=5
结束：j+1=2; i=5
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, -1, 0, 1, 0, 0]
开始：j+1=2; i=6
结束：j+1=3; i=6
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, -1, 0, 1, 2, 0]
// 重点看这里指向 t 和最后的 c的时候回溯
开始：j+1=3; i=7
回溯：j+1=1 // 回溯到g,也就是第一层子串 aga(t)  aga(c)中的ag
// next[j+1] = g != s[i] = c 也就是接着回溯
回溯：j+1=0 // 回溯到a,也就是子串的子串 ag的a
// next[j+1] = a != s[i] = c 也就是接着回溯，判断j < 0 停止回溯
结束：j+1=0; i=7
needle: ["a", "g", "a", "t", "a", "g", "a", "c"]
Next: [-1, -1, 0, -1, 0, 1, 2, -1]
[-1, -1, 0, -1, 0, 1, 2, -1]

图论：有向图

Tech, Study

本文由作者按照 CC BY 4.0 进行授权

数组

二分查找

哈希表

双指针

和字符串和链表的题目有很多重叠的部分

滑动窗口

链表

字符串

28. 找出字符串中第一个匹配项的下标 中等难度 前缀表解法

位运算

堆栈

二叉树相关的都会涉及到一点栈操作

二叉树

二叉树的遍历方式

二叉树的属性

二叉树的修改和改造

求二叉树的属性

二叉树公共祖先问题

二叉搜索树的修改与构造

回溯算法

贪心算法

前缀表

图论：有向图

热门标签

28. 找出字符串中第一个匹配项的下标中等难度前缀表解法